
Özet
Bu çalışmada B-Spline eğri yaklaşımında parametrelerin hesaplanması için derin öğrenmeyi kullanan bir yöntem sunulmaktadır. Var olan yöntemler parametrik değerlerin hesaplanmasını ve düğüm vektörleri ayrı problemler olarak düşünür. Parametrik değerleri ve düğümleri tahmin etmek için birbirine bağımlı derin sinir ağları eğitmeyi öneriyoruz. B-Spline eğri yaklaşımına doğrudan sinir ağları mimarisini eklemenin mümkün olduğunu gösteriyoruz. Parametreleştirme sonuçları sıkı yaklaşımlar verir ve son teknoloji yöntemlerinden daha iyi performans gösterebilir.
1. Giriş
B-spline eğri yaklaşımının parametreleştirilmesi hem parametre değerleri hem de uygun düğüm vektörü hesaplanmalıdır. Parametreleştirmenin büyük ölçüde kaliteli yaklaşımlara bağlı olması birçok uygulama için temel problemdir. Ancak, iyi parametreleştirmeler bulmak karmaşık bir görevdir ve hesaplaması zordur. İyi bir parametreleştirme veri noktası ve yaklaşan eğri arasında minimum sapmayı oluşturan düğüm vektörü ve veri noktasıyla ilişkili parametrik değerlerin bir kümesi olarak tanımlanabilir. Genelde, bir hata eşiğinin tahmin edilmesi gerekir. Ek olarak, yaklaşım mümkün olduğu kadar az kontrol noktası ile sonuçlanmalıdır. Böylece düğümlerin sayısı önemsiz kalmalı.
Genellikle, bir nokta parametresini yeniden bulmak ve uygun düğün noktası hesaplamak ayrı problemler olarak kabul edilir. Nokta parametreleştirmesi çoğunlukla sadece gizli bir düğüm vektörüne yol açan interpolasyon açısından analiz edilir, aksi halde yaklaşım durumunda düğüm vektörü çoğu kez sabit olarak yeniden bulunur. Bir ön işleme adımında iyi bilinen nokta parametresi seçilirken diğer yöntemler düğüm vektörü hesaplamasına odaklanır.
Biz birbirine bağlı iki derin sinir ağını kullanarak düğümleri ve parametrik değerleri aynı anda tahmin eden bir yöntem öneriyoruz (DNN): (1) Nokta Parametre Ağı (PPN) nokta dizilerine parametrik değer atayan; (2) Düğün Seçim Ağı (KSN) düğüm vektörü gelişimi için düğüm değerlerinin tahmin edilmesi. Sinir ağlarımız ara özelliklerin hesaplanmasına ihtiyaç duymadan nokta veri üzerinde doğrudan işler. Ağ mimarisinin içine doğrudan B-spline eğri yaklaşımını dahil etmenin mümkün olduğunu göstereceğiz. Son teknoloji yöntemleriyle karşılaştırdığımızda, parametremiz de yaklaşım hataları daha önemsizdir. Bildiğimiz kadarıyla ilk önce B-spline eğri yaklaşımı için sinir ağlarının potansiyelini göstereceğiz.
2. İlgili Çalışmalar
Çoğu düğüm yerleştirme yöntemleri parametrik değerlerin önceden hesaplanmasını gerektirir. Tekdüze parametrizasyon ve akor uzunluğu parametrizasyonu gibi klasik yöntemlerin yanı sıra en önemli olanı merkezcil yöntemdir [11]. Bir başka çok iyi bilinen yaklaşım yöntemi Lim [13] tarafından önerilen afin değişmezliğine sebep olan ve tek düze yöntemle yakından ilgi olan evrensel metottur. Shamsuddin [24] tarafından önerilen hibrit metot akor uzunluğu ve biraz daha yüksek doğruluklara yol açan merkezcil yöntemlerin karışımıdır. Düğüm yerleştirme genellikle bir hata doymuşluk durumu oluşana kadar yeni düğümlerin eklendiği tekrarlı bir işlemdir. Açısal ölçüye dayalı sezgisel bir kural uygun düğüm değerlerinin belirlemek için kullanılır. Düğüm vektörü hesaplaması için farklı geometrik özelliklerin etkisinin kapsamlı hesaplaması Razdan tarafından verilmektedir [22]. Piegl ve Tiller [19] düğüm vektörlerini oluşturmak için parametrik değerlere ulaşır. Park ve Lee tarafından tanıtılan ünlü bir iyileştirme tabanlı yöntemde düğüm vektörü özel ilgi noktası olan baskın noktaların hesaplanmasına dayanır. Bir makine öğrenimi yaklaşımının düğüm iyileşmesi için destek vektör makinelerini kullanarak [10] Park ve Lee’nin yönteminden daha yüksek hata oranlarıyla yaklaşımlar ürettiği açıklanır [18]. Diğer bir metot düğüm vektör optimizasyonu için genetik algoritmaları ya da ateş böceği algoritması odaklı bir yaklaşım gibi meta-sezgisel algoritmaları kullanır [4].
Makine öğrenimi geometri işleme önemli bir alan haline geldi ve geometrik modellemeyle ilgili farklı problemlere başarıyla uygulandı. Steinke [26] yeniden baş oluşturmak, uç değeri çıkarmak ve boşlukları doldurmak için destek vektör dönüşünü kullanır. Lin [14] 2D resimlere dayalı yeniden oluşturulan yüzey için DNN’leri öneriyor. Qin [21] bir ara temsilci olmadan DNN’lerin sınıflandırabileceğini ya da nokta verilerin bölümlenebileceğini gösterdi. Başka bir önemli araştırma alanı da şekil eşleştirmede [17, 1] ya da şekil tamamlamada [15] Öklid dışı uzayda makine öğreniminin uygulanmasıdır.
3. Ön Bilgiler
Bu bölümde B-spline eğri yaklaşımını ve derin sinir ağlarını kısaca anlatıyoruz.
3.1 B-spline Eğri Yaklaşımı
Her noktanın pi = (xi, yi) koordinatlarıyla temsil edildiği bir nokta dizisi varsayalım p = (p0, …, pm).
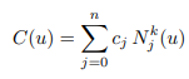
Fonksiyondaki gibi cj kontrol nokraları olan k dereceli, Nik(u) B-spline fonksiyonu ve u0 ve un düğümleri uç nokta ara değerlendirmeleri için k+1 çokluğa sahip azalmayan düğüm vektörü u= (u0, …, un) olan bir B-spline eğrisi düşünün. C yaklaşık p, B-spline eğrisinin cj kontrol noktaları hesaplanarak, önceden hesaplanmış ti i = 0, …, m parametreleriyle en az kareler problemi t = (t0, …, tm) parametre vektörüyle birleştirilmiş ve C(tm) = cn = pm çözülmüştür.
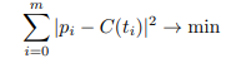
Normal denklem
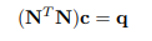
(m – 1) x (n – 1) boyutlu N matris
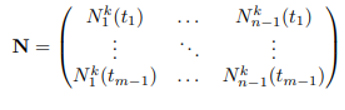
c ve q tanımlı vektörler
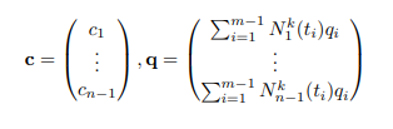
ve i = 1, …, m kadar
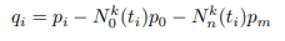
Uç nokta için herhangi bir kısıtlama yoksa şu şekilde azalır.
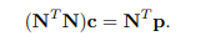
cj kontrol noktaları figür 1’deki denklem kullanarak hesaplanabilir.
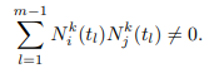
Bu j = k, …, n + 1 için ti ∈ [uj, uj+1] olan bir parametrenin varlığına eşdeğerdir. Bakınız örnek [3]. Deneylerimizde k=3 olarak kullandık.
3.2 Derin Sinir Ağları
Bu çalışmada sıkı B-spline eğri yaklaşımları elde etmek için bir u düğüm vektörü ve p noktalarına göre ileri beslemeli DNN’leri uygularız. DNN’ler düzgün davranan yapay nöronların katmanları halinde düzenlenmiştir. Bu katmanlardan bazıları eğitilebilir, ayarlanabilir ağırlıklarla davranışları kontrol edilebilir. Burada, her nöronun önceki katmanın tüm nöronlarına ağırlıklar aracılığıyla bağlandığı klasik çok katmanlı algılayıcı (MLP) mimarisini (Figür 2) kullanıyoruz. Her nöron girdilerin ağırlıklı toplamını hesaplar ve bir sonraki katmanda bulunan tüm nöronlara bağlanan çıktı olarak doğrusal olmayan statik bir yolla besler. Ağırlıklar, eğitim aşamasında DNN’nin performansını ölçen kayıp fonksiyona gradyan iniş uyarlanır. Derin öğrenmeyi derinlemesine öğrenmek için Goodfellow ve arkadaşlarının tartışmalarına bakabilirsiniz [6].
Parametreleştirme problemimize DNN’leri uygulamak için aşağıdaki zorlukları ele almalıyız.
1. Bu problem için herkese açık veri kümesi olmadığı için, yeterince büyük eğitim veri setleri sentezlemeliyiz.
2. Eğitim verilerinin ve gerçek verilerin aynı özellikleri paylaştığından emin olmalıyız.
3. B-spline yaklaşımının parametreleşmesi için uygun kayıp fonksiyon tanımlanmalıdır.
4. Mimarisi nedeniyle, bir MLP sabit boyutta girdi gerektirirken, yaklaşım için nokta dizileri değişken boyuttadır. Yaklaşım bu sorunla başa çıkabilmelidir.
4.Nokta Parametreleştirilmesini ve Düğüm Yerleştirmesini Öğrenme
Bu bölümde gelişigüzel 2D nokta dizilerine göre düğüm yerleştirmesi ve nokta parametreleştirmesi için yöntemimiz anlatılacaktır. Anlatımımızda parametrelendirme sürecine genel bir bakış sağlayan Figür 1’i takip ediyoruz.
P1. Bölütleme
Giriş nokta dizisi p, pi noktasındaki eğriliği ki olan toplam eğriliği ile verilen bir karmaşıklığa sahiptir.
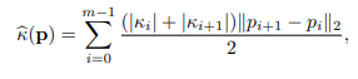
Bu çalışma boyunca eğrilik dokunum çemberi kullanılarak hesaplanmıştır. k(p)’ yi bir karmaşıklık ölçüsü olarak kullanarak, eğitim veri setinin maksimum karmaşıklığını ve bununla DNA’nın işleyebileceği maksimum karmaşıklığı ölçebiliriz. 2. zorluğu işlemek için nokta dizilerini ayırmayı öneriyoruz böylece ortaya çıkan segmentler eğitim verilerinin karmaşıklığını temsil eder. Eğer eşik değeri kt için k(p) > kt ise bir nokta dizisi için p toplam eğriliği c(p) hesaplayın ve p’yi, medyanda ps, s = 1, …, r nokta dizisi segmentlerine bölün. kt’yi eğitim setinin %98’lik dilimine ayarladık. Bu segmentasyon sürecini her segment ps, k(ps) < kt karşılayana kadar r-1 kere tekrarlarız.
P2. Alt / Süper Örnekleme ve Normalleştirme
ps, s = 1, …, r’yi PPN / KSN ile işlemek için segment başına nokta sayısı DNN giriş boyutu l (4.) ile eşleşmelidir. Böylece ps alt veya süper örneklenir.
Alt Örnekleme:
ps cinsinden nokta sayısı l’den büyükse, çizilen indisler i eşit olarak dağıtılır ve ilk ve son noktaları içerecek şekilde ps ‘den noktalar çizilir.
Süper Örnekleme:
Eğer ps ‘nin nokta sayısı l’den daha küçükse ardışık pis ve pi+1s noktaları arasına soldan sağa geçici noktalara doğrusal olarak eklenir. Bu durum noktaların sayısı l’e eşit olana kadar tekrarlanır. Onlar sadece ağ giriş boyutunu eşlemek için vardır.
Alt ve süper örneklenmiş segmentler daha sonra ps’nin minimum ve maksimum koordinatları olan noktalardan oluşan ps ‘ye normalize edilir.
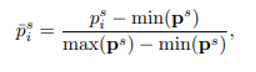
P3. Parametreleştirme
Her bir p için PPN (bkz. Bölüm 5.1) bir parametre ts ⊂ [0, 1] parametrizasyonu üretir. Parametrelendirme [us − 1, us] olarak yeniden ölçeklendirilir ve ps‘nin alt/süper örneklemesi olarak uyarlanır ve ts verir. Alt örneklemede ps‘den çıkarılan bir pi noktası için, ts‘ye bir parametre ekleyin. Burada akorlen, bir nokta dizisi ile tanımlanan çokgenin uzunluğudur ve psa ve ps pi, tsa ve tsb parametreleriyle alt örneklenen segmentte pi‘nin sola ve sağa en yakın komşusudur.
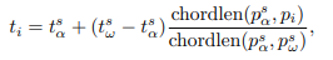
Geçici noktalara karşılık gelen tsi parametreleri ts‘den kaldırılır. Parametrizasyon adımının başlatılması için bir başlangıç düğüm vektörü gereklidir. Önce u0 = 0 ve un = 1’i tanımlayın. Ardından, her segment için (sonuncusu hariç) bir düğüme ui eklenir.
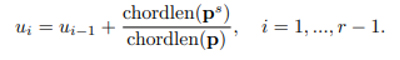
Bu denklem her nokta dizisi segmenti için bir başlangıç ve bitiş düğümünü verir.
P4. Geliştirme
İyileştirme adımında, büyük yaklaşım hatası olan nokta dizisi segmentlerine ek düğümler eklenir. Giriş verilerine p en büyük Hausdorff mesafeli segment ps‘yi belirleriz. ps ve ts için KSN (bkz. Bölüm 5.2) yeni bir tahmini düğüm us ∈ [0, 1] oluşturur. Yeni düğüm us, gerçek düğüm değeri aralığıyla [us − 1, us] şu şekilde eşlenir:
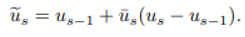
Daha sonra, us yerine, us‘e en yakın parametre değeri ti, u’ya eklenir. KSN alt / süper örneklenmiş veriler üzerinde çalıştığından, bu kullanıcı arabirimlerinin düzeltilmesi en basit seçimdir (3).
Açıklama 1: Unutmayın, karşılandığı sürece us doğrudan u’ya eklenebilir (3). İstenen eğri yaklaşım hata eşiği karşılanana kadar u’yu daha da iyileştirmeyi öneriyoruz.
5. DNN Mimarisi
Bu bölümde, nokta parametrelendirme (PPN) ve düğüm seçimi (KSN) için derin sinir ağları mimarilerini ve bunların eğitimini açıklıyoruz. Figür 2, bu ağların ağ mimarilerini göstermektedir.
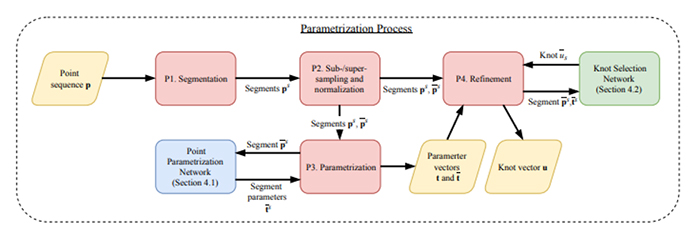
Figür 1: Parametrizasyon sürecine genel bakış. Girişler / çıkışlar sarı ile işaretlenmiştir. Kırmızı kutular, Bölüm 4’te art arda açıklanan alt işlemlere atıfta bulunur. Diğer renkler, Figür 2’deki alt işlemlere atıfta bulunur.
Bu ağlar girdi olarak nokta dizisi segmentlerini ps aldığından, gösterimi basitleştirmek için Bölüm 5.1 ve 5.2’deki tüm değişkenler için üst indeks s ve üst çubuğu bırakacağız.
5.1. Nokta Parametreleştirme Ağı
p noktası dizisi için bir t = (ti)i parametre vektörü ti = ti-1 + ∆i-1 olarak tanımlanır. Klasik yöntemler için ∆i, p’nin geometrik özelliklerine göre hesaplanır, örn. merkezcil parametrizasyonu![]()
Nokta parametrizasyonu ağı adı verilen önceden eğitilmiş bir sinir ağı kullanarak ∆i’yi tahmin etmeyi öneriyoruz. Benzer şekilde, PPN’nin girdisi bölümleri p’den oluşur. p = (xo, …, xl-1, y0, …, yl-1) biçiminde yazılabilir, burada x ve y p noktalarının koordinatlarıdır. Parametre alanı u0 = t0 = 0 ve un = tl-1 = 1 olarak tanımlanır.
Daha sonra, PPN’nin görevi, eksik değerleri ∆ = (∆0, …, ∆l-2) ile tahmin etmektir, öyle ki t0 <t1 ve tl-2 <tl-1.
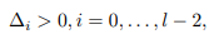
Girdi verilerine bir MLP uygularız ve çıktı olarak parametreleştirme için bir dağılım veririz. Boyut l-1 için;
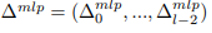
PP1. Biriktirme ve Yeniden Ölçeklendirme
∆mlp çıktısı, tmlp0 = 0 olan bir parametre vektörü tmlp‘yi hesaplamak için kullanılır.
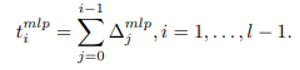
tl-1mlp genellikle 1 olmadığından, tmlp‘nin yeniden ölçeklendirilmesi son parametre vektörü t’yi aşağıdaki denklem verir.
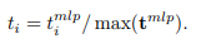
(4) ‘ü sağlamak için, MLP çıktısı ∆mlp pozitif olmalıdır. Bu, PPN’deki MLP’nin nöronları için softplus aktivasyon fonksiyonu kullanılarak elde edilir.
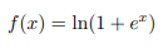
PP2. Yaklaşım
Bir ağ kaybını (CL3.) Tanımlayabilmek için, B-spline eğri yaklaşımını doğrudan bir ağ katmanı olarak dahil ediyoruz. Giriş noktaları p ve parametreleri t, k = 3 için u = (0, 0, 0, 0, 1, 1, 1, 1) düğüm vektörü ile yaklaşım için kullanılır. PPN, tüm eğriyi değil de eğri segmentlerini parametreleştirdiği için, son nokta enterpolasyonu (2) olmadan yaklaşıyoruz. Yaklaşım katmanının çıktısı papp = (p0app ,.., pl-1app) t’de değerlendirilen yaklaşık B spline eğrisidir.
PP3. Öklid Kaybı
PPN için kayıp
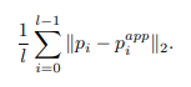
5.2. Düğüm Seçim Ağı
KSN, belirli bir segment p ve parametreleri t (PPN tarafından tahmin edilen) için aralığa (0, 1) yeni bir u düğümünü tahmin eder. Böylece ortaya çıkan ağ giriş boyutu 3l’dir. Girişe tek bir çıkış değeri umlp‘ye dönüştüren bir MLP uygularız. Ağ aktivasyon fonksiyonları olarak Sigmoid fonksiyonunu [7] kullandığımız çıktı katmanı dışında RELU fonksiyonunu [5] kullanırız.
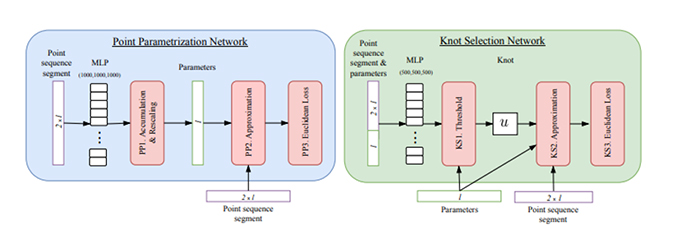
Figür 2: Nokta Parametrelendirme Ağı (PPN, sol) ve Düğüm Seçim Ağı (KSN, sağ) için ağ mimarileri. Kırmızı kutular, Bölüm 5.1 ve 5.2’de arka arkaya açıklanan alt işlemlere atıfta bulunmaktadır.
KS1. Eşik Katmanı
(3)‘deki denklemi sağlamak için yeni u düğümünün u ∈ (0, 1) ve t ∩ [0, u] ≠ ∅ ve t ∩ [u, 1] ≠ ∅ ‘yi sağlaması gerekir. Bu kısıtlamaları karşılamak için umlp‘yi şu şekilde eşleyen bir eşik katmanı kullanıyoruz:
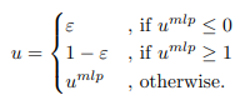
Küçük bir ε = 1e − 5 ekleyerek son düğümlerdeki düğüm çokluğunun k’ye eşit kaldığından emin oluruz. Bu u seçimi, Açıklama 1’de bahsedilenden daha genel bir yaklaşıma karşılık gelir.
KS2. Yaklaşıklık
KSN’deki yaklaşım, düğüm vektörü haricinde PPN’nin yaklaşımı ile aynı forma sahiptir. Burada düğüm vektörü u = (0, 0, 0, 0, u, 1, 1, 1, 1). Geri yayılım için, B-spline temel fonksiyonlarının u’ya göre türevi gereklidir, bkz. [20]. PPN’ye gelince, yaklaşım katmanının çıktısı papp = (p0app, …, pl-1app) t’de değerlendirilen yaklaşık B-spline eğrisidir.
KS3. Öklid Kaybı
KSN için kayıp fonksiyonu PPN ile aynıdır, bkz. (5).
5.3. Eğitim seti oluşturma ve eğitim süreci
PPN ve KSN’nin eğitimi için yeterince büyük eğitim ve test veri kümeleri gereklidir. Girdi boyutunu, l = 100 olarak tanımlıyoruz. İdeal bir veri kümesi, bilinen sıralı bir nokta sırasına sahip çeşitli gerçek dünya nokta bulutlarından oluşacaktır. Bu tür veri kümeleri genel olmadığından, verileri B-spline eğrilerini kullanarak sentezlemeyi seçtik. Ortalama µ ile normal bir dağılım kullanarak ci rasgele kontrol noktaları oluşturuyoruz ve k = 3 dereceli B-spline eğrilerini (k + 1) -kat uç düğümleriyle ve iç düğümler olmadan tanımlamak için σ değişkenliğini kullanıyoruz. Y koordinatları için, σ = 2 ve µ = 10’u kullanırız. X koordinatları için, ilk kontrol noktası için σ = 1 ve µ = 10’u kullanırız ve tüm ardışık kontrol noktaları için µ’yu ∆µ = 1 olarak arttırırız. Kendi kendine kesişimleri olan eğriler atılır, çünkü aynı noktaların sıralı sırası benzersiz değildir ve tersine mühendislikte, bu tür nokta kümeleri genellikle kendi kendine kesişimde alt kümelere ayrılır. Kontrol noktası x koordinatları için daha küçük σ, ilk etapta kendi kendine kesişim içeren eğrilerin sayısını azaltır. Bu yaklaşımı kullanarak 150.000 eğriden oluşan bir veri seti oluştururuz. Sonra, her eğri boyunca p = (p0 ,…, pl-1) noktalarını örneklendiririz. Bu eğriler, soldan sağa artan x koordinatlarına sahip olma eğiliminde olduklarından, veri kümesine nokta dizilerinin indekslenmiş versiyonlarını ekleriz ve bunun sonucunda % 20’si eğitim sürecinde test verileri olarak kullanılan 300.000 nokta sekansı elde edilir. Deneylerimizde, bu yöntem, çok az eğriliğe sahip veya hiç olmayan bölümler ile yüksek eğriliğe ve hatta keskin özelliklere sahip bölümler içeren çok çeşitli eğriler kümesine yol açar. Veri kümesi üretimi için kübik B-spline eğrileri kullanırken, yaklaşımımız bu şekilde hesaplanan nokta bulutlarıyla sınırlı değildir.
KSN, girdi olarak t nokta parametrelendirmeleri gerektirdiğinden, ilk olarak PPN eğitilir. Eğitimden sonra, PP2 ve PP3 katmanları atılır ve PP1 ağ çıkış katmanı olur. PPN’yi uygulayarak eğitim veri seti için t parametrik değerleri hesaplıyoruz ve KSN’yi birleşik giriş üzerinde eğitiyoruz. Bölüm 4’teki parametrelendirme için KS2 ve KS3 katmanları atılırken KS1 ağ çıkış katmanı olur. PPN ve KSN’nin MLP’leri (1000, 1000, 1000) ve (500, 500, 500) boyutlarında üç gizli katmandan oluşur. Figür 3, eğitim sürecinin bir özetini vermektedir. Bırakmayı [8] MLP katmanlarına uyguluyoruz ve Adam optimizer [9] kullanarak ağları eğitiyoruz.
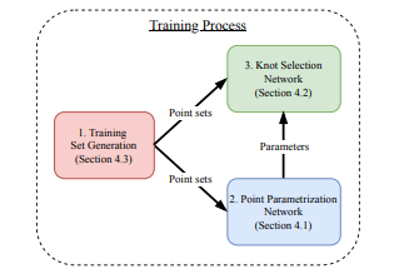
Şekil 3: Eğitim sürecine genel bakış. Kırmızı kutu bölüm 5.3’teki eğitim seti oluşturmayı ifade eder. Diğer renkler bölüm 4.
6. Sonuçlar
Bu bölümde PARNET dediğimiz parametrizasyon yöntemimizin sonuçlarını sunuyoruz. İlk olarak, PPN tarafından hesaplanan nokta parametrelendirmelerinin sonuçlarını tartışıyoruz (Bölüm 6.1). Ardından, KSN tarafından hesaplanan düğüm seçimlerinin yanı sıra yaklaşımımızın genel yaklaşım kalitesini tartışıyoruz (Bölüm 6.2). Değerlendirme için dört değerlendirme seti oluşturduk:
- Değerlendirme seti 1, Bölüm 5.3’te açıklandığı gibi hesaplanan 500 eğri içerir. Her eğri üzerinde eşit dağıtılmış (yay uzunluğu açısından) 500 nokta örnekliyoruz.
- Değerlendirme seti 2, değerlendirme seti 1’den gelen eğrileri içerir, ancak rastgele parametrelerde örneklenir.
- Değerlendirme seti 3, Bölüm 5.3’te açıklandığı gibi hesaplanan ancak çokluklar içermeyen rastgele iç düğümlerle hesaplanan 500 eğri içerir. Bazıları yüksek karmaşıklıktaki çok çeşitli eğrilerle sonuçlanan 3 ila 8 rastgele iç düğüm üretiriz. Her eğri üzerinde eşit dağıtılmış 500 noktayı örnekliyoruz.
- Değerlendirme seti 4, değerlendirme seti 3’ten gelen eğrileri içerir, ancak rastgele parametrelerde örneklenir.
Değerlendirme seti 2 ve değerlendirme seti 4’ü değerlendirmemize dahil ettik çünkü birçok parametreleme yöntemi parametreleştirmeden önce gürültü filtreleri kullanır, örn. [23]. Bu filtreler düzgün bir nokta kümesi (veya düzgün eğrilik) ile sonuçlanır, ancak aynı zamanda noktaların eşit olmayan dağılımına da yol açar. Eğitim, test ve değerlendirme setleri (http://www.ios.htwgkonstanz.de/parnetdatasets) adresinden indirilebilir.
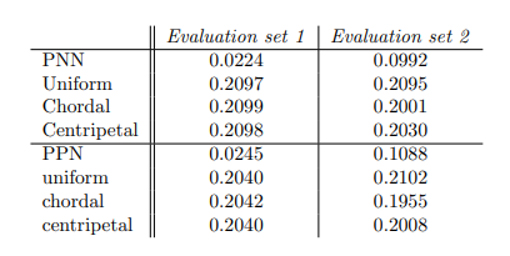
Tablo 1: Yaygın parametreleştirme yöntemlerine kıyasla PPN’nin iç düğümleri olmadan yaklaşım için ortalama Hausdorff mesafeleri.
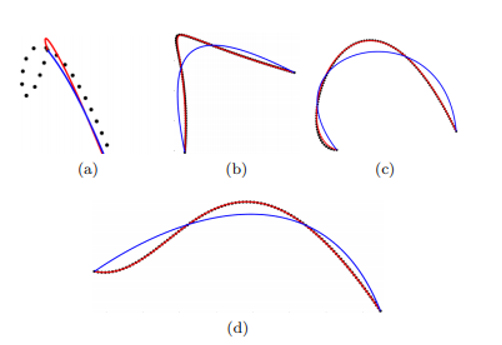
Şekil 4: Merkezcil yöntem (mavi) ve PPN (kırmızı) ile değerlendirme seti 1 örnekleri için iç düğümler olmadan yaklaşık parametrelendirmelerin sonuçları.
6.1. Nokta Parametrizasyonu
Tablo 1’de PPN tarafından hesaplanan nokta parametrelerini ve tekdüze, kordal ve merkezcil parametrelendirmeyi karşılaştırıyoruz. Eğri yaklaşım kalitesinin değerlendirilmesi için Hausdorff mesafesi fiili standarttır [25, 2]. Tüm değerlendirme setindeki ortalama Hausdorff mesafesi açısından eşit dağıtılmış ve rastgele örneklenmiş noktalar için yöntemleri karşılaştırıyoruz. PPN tarafından hesaplanan parametreler, değerlendirme seti 1 için sekiz kata kadar daha küçük Hausdorff mesafeli yaklaşımlarla sonuçlanır. Değerlendirme seti 2 için sonuçlar, diğer yöntemlerle karşılaştırıldığında hala iki kat daha küçüktür. Parametrelendirme için çoğu yöntem, noktaların geometrik ilişkilerine dayanır. Yüksek eğriliğin daha yoğun bir parametrizasyon için güçlü bir gösterge olduğu gösterilmiştir [16]. [11] ‘de Lee, merkezcil parametrizasyonu da içeren genel üs yöntemini tanıttı. Burada parametre değerleri, eğrilikteki değişikliklere dayanmaktadır. Daha yüksek eğriliğe sahip bölgelerin daha yoğun örneklendiği varsayıldığında, Tablo 1 ve Şekil 4’teki sonuçlardan da görülebileceği gibi, bu yöntem eşit dağıtılmış noktalar için başarısız olmaktadır. Figür 4’de merkezcil yönteme kıyasla PPN’nin daha büyük Hausdorff mesafesine yol açtığı bir örneğin yakından görünüşünü gösterir. Figür 5’te, parametrelendirmenin ∆ dağılımına göre değerlendirme seti 1’de eğrileri renklendirdik.

Figür 5: Değerlendirme seti 3’ün ısı haritası renkli eğrileri parametrizasyon değeri ile renklendirilmiştir. Mavi, ∆ için düşük değerlere karşılık gelirken kırmızı, ∆ için büyük değerlere karşılık gelir.
Büyük bir mutlak eğriliğin, ∆’daki daha büyük değerler için güçlü bir gösterge olduğu açıktır. Ancak bükülme noktaları içeren bölgeler de ∆ ‘de büyük değerlere yol açar. Değerlendirme seti 3’teki noktalar eşit dağıtıldığından PPN, eğriliği parametrizasyon sürecine dahil etmeyi öğrenmiştir.
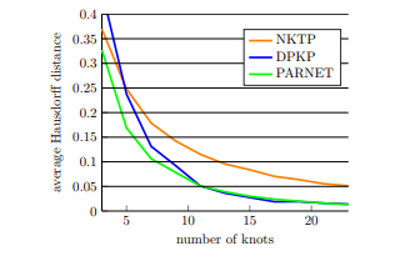
Figür 6: PARNET, DPKP ve NKTP için farklı düğüm sayılarında değerlendirme seti 3 üzerinden ortalama Hausdorff mesafesi
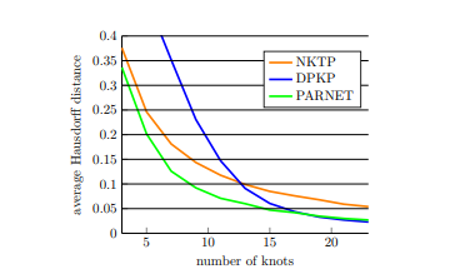
Figür 7: PARNET, DPKP ve NKTP için farklı düğüm sayılarında değerlendirme seti 4 üzerinden ortalama Hausdorff mesafesi
6.2. Düğüm Seçimi
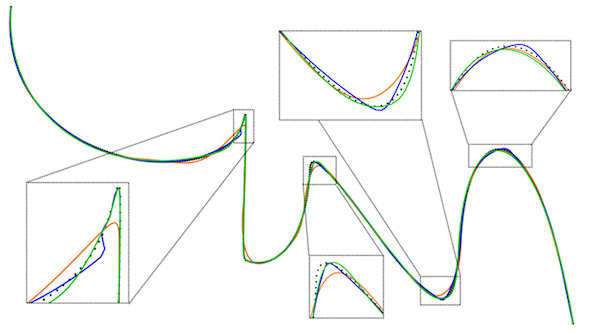
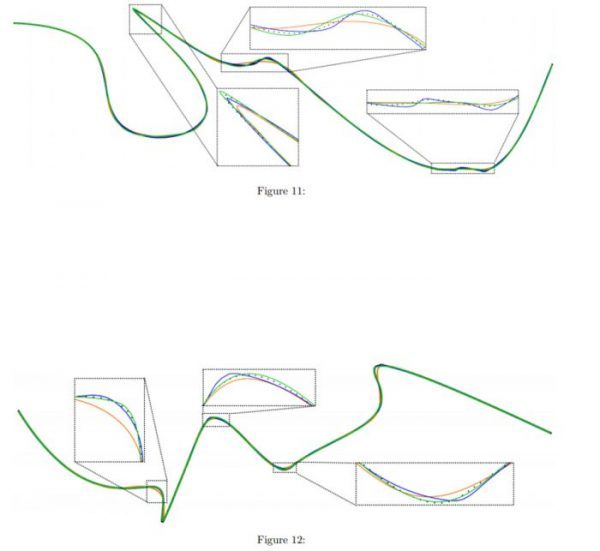
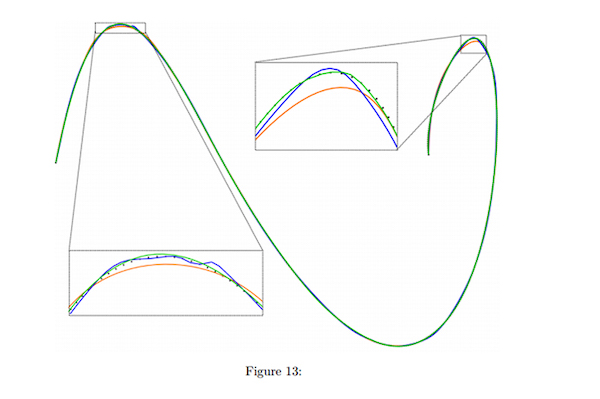
Yaklaşımımızın etkinliğini PARNET’i diğer iki düğüm yerleştirme yöntemiyle karşılaştırarak değerlendiriyoruz. Bunlardan biri, düğüm yerleştirme (NKTP) sürecine herhangi bir geometrik bilgiyi dahil etmeyen, Piegl ve Tiller [20] tarafından iyi bilinen bir ortalama alma yöntemidir. İyileştirme kullanarak düğümler yerleştirdiğimiz için PARNET’i Park ve arkadaşları tarafından iyi bilinen iyileştirme tabanlı bir yöntemle de karşılaştırıyoruz. [18] Düğüm yerleştirme için baskın noktaları (DPKP) kullanır. Yine, yöntemler ortalama Haussdorf mesafesi ile karşılaştırılır. Figür 5 ve 7, değerlendirme setleri 1 ve 2’de 3 ila 23 düğüm aralığında düğüm yerleştirme sonuçlarını gösterir. Her iki settede, yöntemimiz daha yüksek kalitede yaklaşık değerler üretir. Özellikle 3 ila 12 düğüm aralığında daha az düğüm olduğunda, yöntemimiz önemli ölçüde daha düşük Haussdorf mesafesine sahiptir. Artan düğüm sayısıyla, DPKP ve yöntemimizin sonuçları, değerlendirme seti 3’teki 23 düğümdeki yöntemimiz ve değerlendirme seti 4’teki DPKP için küçük bir farkla çok yakındır. Figür 8, bir örnek için farklı yöntemlerle yaklaşımı gösterir. Değerlendirme setinden 3. NKTP çok düzgün sonuçlar verirken karmaşık bölgelerde başarısız olur. DPKP yöntemi, yüksek eğrilik bölgelerini çok iyi bir şekilde yaklaştırabilir ancak bu bölgelerde kıpırdanmalara da yol açabilir. Metodumuz, oldukça eğimli bölgeleri yaklaşık olarak belirleyebilir ve aynı zamanda yumuşak yaklaşımlar üretebilir (daha fazla örnek için ek montaj ilişkisine bakın). Figür 9’da KSN tarafından iyileştirme için değerlendirme seti 1 ve tahmin edilen düğüm konumlarının bazı eğrilerini sunuyoruz. KSN tarafından yapılan düğüm tahminlerini inceleyerek, diğer yazarların gözlemlerine uyan birkaç gözlem yapıyoruz:
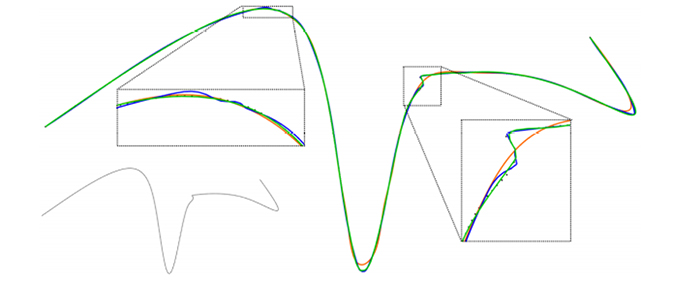
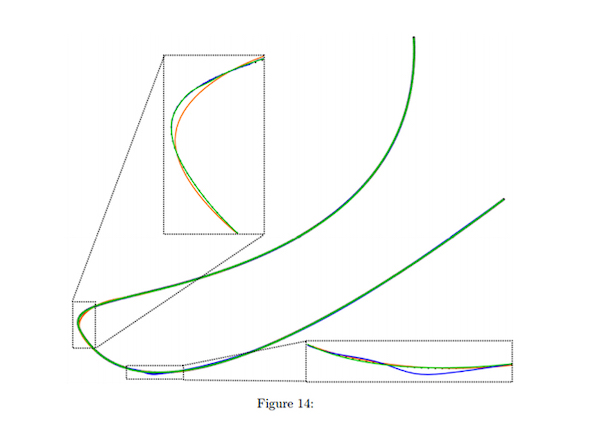
Figür 8: NKTP (turuncu), DPK (mavi) ve PARNET (yeşil) yöntemlerine göre değerlendirme seti 3’ün bir örneği için 23 düğümlü yaklaşım sonuçları. Orijinal nokta dizisi sol alt köşede gösterilirken, çerçeveli kutular kritik bölgelerin yakın çekimlerini içerir.
- Eğrilik düğüm yerleştirmede önemli bir rol oynar [22, 31]. Düğümler yerleştirilirken yüksek kavisli bölgeler tercih edilmelidir (bkz. Figür 9b, 9c, 9d ve 9e).
- Değişken eğrilik yönlerine sahip segmentleri rafine etmek gerekirse, düğümü bir bükülme noktasına yerleştirmek faydalıdır [10, 18]. KSN’nin düğümü yüksek kavisli bölgelere değil bir bükülme noktasına yakın yerleştirmeyi seçmesinin örnekleri, Şekil 9f ve 9h’de görülebilir.
- Eğrilik küçükse veya yavaş değişiyorsa, segmentlerin bölünmesi yararlıdır, böylece ortaya çıkan segmentler eşit karmaşıklıkta olur [18, 22]. Bu, KSN’nin nokta setlerini medyan indekse yakın böldüğü, ancak daha yüksek kavis içeren segmentleri daha küçük hale getirdiği Figür 9a ve 9g’de görülebilir.
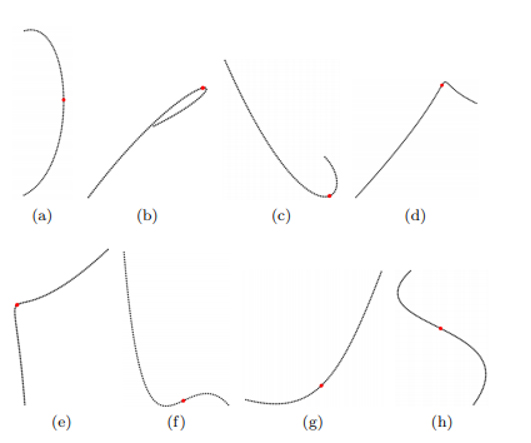
Figür 9: Değerlendirme seti 1’in numunelerinde KSN tarafından seçilen tek düğüm (kırmızı).
7. Tartışma
Deneylerimiz, sinir ağlarının B-spline eğri yaklaşımı problemi için aynı anda parametrik değerleri t ve u düğümlerini başarılı bir şekilde tahmin edebildiğini göstermektedir. Bizim yöntemimiz sıkı tahminlerle sonuçlanır. Eşit aralıklı nokta dizileri üzerinde eğitim almamıza rağmen, eşit olmayan aralıklı noktalarda da iyi çalışır. Bu, ağımızın çok yönlü özelliklere sahip daha önce görülmemiş verilere iyi bir şekilde genelleyebildiğini göstermektedir. Yaklaşımımızı sınırlayan bir husus, sentetik eğitim veri setidir. Gerçek dünya verileri tercih edilebilir. Uzmanlaşma amacıyla ağları yeniden eğitmek yaygın olduğundan, yaklaşımımız daha sonra ek veriler üzerinde iyileştirilebilecek bir ön eğitim yöntemi olarak kullanılabilir. Metodumuzun bir başka dezavantajı, nokta dizilerinin alt ve üst örneklemesinin yanı sıra segmentasyon ihtiyacıdır. Yaklaşım kalitesinin ön işlemenin bir sonucu olmadığını, ağlar tarafından parametreleştirmenin bir sonucu olduğunu göstermek için kasıtlı olarak çok basit bir şekilde segmentlere ayırmayı ve örneklemeyi seçtik. Yaklaşımımızda B-spline eğri yaklaşımı doğrudan ağ eğitim döngüsüne entegre edilmiştir. Bunun, diğerlerinin yaklaşımla ilgili sorunlar için sinir ağlarını uygulamasına olanak sağlayacağını umuyoruz. Gelecekteki çalışmalarda, segmentasyon ve örneklemeden daha bağımsız olmak için tekrarlayan ağlar gibi yöntemleri dikkatle araştırmayı planlıyoruz. Ayrıca yüzey yaklaşımı ve T-spline gibi diğer parametrik gösterimlere yaklaşımımızı uygulamak istiyoruz.